The Potemkin Argument, Part 6: The Erratic Disciples of Dr. John Carlisle

This is a public peer review of Scott Alexander’s essay on ivermectin, of which this is the sixth part. You can find an index containing all the articles in this series here.

For this post, I will focus on a particular method he relies on in his criticism of several papers, and a favorite of the “fraud hunters” squad, upon whose work he builds.

In his article, Scott writes:

Part of this new toolset is to check for fraud. About 10 - 15% of the seemingly-good studies on ivermectin ended up extremely suspicious for fraud. Elgazzar, Carvallo, Niaee, Cadegiani, Samaha. There are ways to check for this even when you don’t have the raw data. Like:

• The Carlisle-Stouffer-Fisher method: Check some large group of comparisons, usually the Table 1 of an RCT where they compare the demographic characteristics of the control and experimental groups, for reasonable p-values. Real data will have p-values all over the map; one in every ten comparisons will have a p-value of 0.1 or less. Fakers seem bad at this and usually give everything a nice safe p-value like 0.8 or 0.9.

• GRIM - make sure means are possible given the number of numbers involved. For example, if a paper reports analyzing 10 patients and finding that 27% of them recovered, something has gone wrong. One possible thing that could have gone wrong is that the data are made up. Another possible thing is that they’re not giving the full story about how many patients dropped out when. But something is wrong.

Before we move on, a sidebar: Scott notes that 10-15% of studies ended up “suspicious for fraud.” In case a reader takes this surprising number as a massive blow for ivermectin—indicating a low-quality evidence base—do keep in mind that this percentage is actually on the low-end of what most people expect of clinical trials in general. Richard Smith, former editor of the British Medical Journal, in his article, “Time to assume that health research is fraudulent until proven otherwise?” writes:

Ioannidis concluded that there are hundreds of thousands of zombie trials published from those countries alone.

Others have found similar results, and Mol’s best guess is that about 20% of trials are false. Very few of these papers are retracted.

You’ll observe that despite the constant noise to the contrary, the level of bad studies in the ivermectin literature—especially given the diverse origins and extremely deep scrutiny—is not actually out of the ordinary. This is a general problem of clinical research—being pinned on ivermectin, as if to make a point—but the evidence just isn’t there.

Before we get into the specifics of the papers Scott mischaracterizes, it’s important to dive into the Carlisle method, in order to get some context about where his claims are coming from.

Carlisle’s Statistical Dragnet

In the last few years, the quest for statistical ways to check for academic fraud has become a very active arena. Much of this has been spurred on by the work of Dr. John Carlisle, who has single-handedly applied his method to thousands of papers, finding very suspicious patterns in more than 100 publications. His work has led to several retractions of published randomized trials. His method essentially consists of finding differences in the baseline continuous variables of randomized trials that are so large, they would be incredibly unlikely to occur in a properly randomized trial. The statistical threshold he uses to make a claim against a trial is to have a finding of less than 1/10,000 chance of appearing by chance.

In his seminal publication, Carlisle is extremely careful to note that his methods catch all sorts of errors, and should not be immediately considered evidence of academic fraud or fabrication:

Some trials with extreme p values probably contained unintentional typographical errors, such as the description of standard error as standard deviation and vice versa. The more extreme the p value the more likely there is to be an error (mine or the authors’), either unintentional or fabrication

Several other statisticians have chimed in, noting that Carlisle makes some assumptions that are not actually true. To summarize Stephen Senn:

• baseline variables should not assumed to be independent

• distribution of p-values in published randomized trials is not uniform

• randomization is not always “pure” (e.g. many trials use block randomization)

These concerns don’t invalidate Carlisle’s work, but they do create a context within which its findings must be carefully considered on a case-by-case basis. F. Perry Wilson, in his excellent analysis of the Carlisle method summarizes it thusly:

With that in mind, what Carlisle has here is a screening test, not a diagnostic test. And it’s not a great screening test at that. His criteria would catch 15% of papers that were retracted, but that means that 85% slipped through the cracks. Meanwhile, this dragnet is sweeping up a bunch of papers where sleep-deprived medical residents made a transcription error when copying values into excel.  

I want to stress that I’m not saying the method Carlisle has pioneered is useless. It has led to genuine fraud being discovered, for example in the case of Italian surgeon Mario Schietroma, whose trials consistently threw up red flags. It is, however, extremely important to understand what claims it enables one to make, and what shaky assumptions it requires one to accept. Carlisle’s tests are a starting point for further investigation, not a one-step conviction for academic fraud.

Checkhov’s Footgun

The reason we can’t have nice things is because a tool that is extremely easy to use is a tool that is extremely easy to abuse. The example I know the best is also the most relevant to the topic at hand: Dr. Kyle Sheldrick, on whom Scott relies for several of the claims in his essay, accused Dr. Paul Marik of “audacious fraud,” on the basis of an improvised variation of the Carlisle method. The accusation? That Marik’s data is unlikely on the order of “trillions to quadrillions to one”:

This actually presents a slight problem in estimating how unlikely these results are, as the most common test for fraud in this situation would be the Stouff-Fisher, but this will declare these results infinitely unlikely (as the majority of variables have a p value of exactly 1), when in reality it is probably more likely that it is no more than trillions to quadrillions to one.

The problem? Not only did he not fully appreciate the assumptions listed above, but he applied the method to a non-randomized trial; not on continuous variables as Carlisle did. Sheldrick did attempt to correct for these issues. However, that’s where things started to go terribly wrong. Upon being challenged by statistician Mathew Crawford, Sheldrick partially corrected his calculations, revising his conclusion of improbability way down:

In this section the author points out that for "malignancy" the chance of getting a p value over 0.4 is more than 60% and these might add up to an order of magnitude over a set of 22 variables. I agree which is why I said it was "quick and dirty" rather than calculating the exact likelihood for each. For the record this is the exact value for every variable of p >0.4 and their product. It does indeed reduce the risk from being on the order of 1 in 100,000 to being on the order of 1 in 10,000. This seems a lot like nit-picking at the edges. 

To make matters worse, mathematician Daniel Victor Tausk corrected Sheldrick again in the comments:

Here I just want to comment on what you said in this sentence:

"It does indeed reduce the risk from being on the order of 1 in 100,000 to being on the order of 1 in 10,000. This seems a lot like nit-picking at the edges."

which is not really fair. The probability actually increases from 1 in 106083 to 1 in 3345 (see minor technical remark and code below), which is a substantial difference. Your original post also talks about probabilities of the order of "trillions to quadrillions to one," which are completely wrong.

With the finding being down to 1 in 3345 (still with most of Carlisle’s shaky assumptions uncorrected), Sheldrick’s finding is now at about 1/3 of the threshold that Carlisle had set for raising the “improbability” alert. Further in the comments, Tausk reveals that when correcting some of the issues inherent in Carlisle’s method, he gets down to 1/490—and that’s a number that could be lower still. In other words, Carlisle would never even have said anything at all about that paper. Instead, Sheldrick wrote an open letter to the journal—without even bothering to contact Marik first, one of the world’s most published critical care doctors—for clarification.

It should be unsurprising then that after legal action was taken against him, Sheldrick took the original blogpost down, and took his profile on Twitter private for a time. Professor Norman Fenton has a very readable, if devastating, takedown of Sheldrick’s accusations if you want to read more on this.

Scott Alexander’s Game of Telephone

Much like in Part I of this series, Scott takes the word of someone presented as an authority by the press, and cranks up the volume by an order of magnitude. In this case, we’ll look at how he takes the claims of Sheldrick, as well as the methods of Carlisle, and applies them with far less elegance than Carlisle or even Sheldrick, to horrifying effect.

I. Cadegiani, Again

For example, in the case of Flavio Cadegiani, even after correcting the most egregious errors, he still writes the following:

Speaking of low p-values, some people did fraud-detection tests on another of Cadegiani’s COVID-19 studies and got values like p < 8.24E-11 in favor of it being fraudulent.

As you’ll understand if you’ve read this far, the test that was run was not “fraud-detection,” and it did not (and could not) conclude that what it picked up was “fraudulent.” Scott continues to present his readers with allegations against working doctors and researchers that would not be put forth by anyone who understands the methods in use here. Even though I’ve let him know that his fraud allegations are gross exaggerations unsupported by the underlying theory, the fraud claim is still in place.

II. Ghaury et al.

Another study unfairly maligned is Ghaury et al., which is described as follows:

Ghauri et al: Pakistan, 95 patients. Nonrandom; the study compared patients who happened to be given ivermectin (along with hydroxychloroquine and azithromycin) vs. patients who were just given the latter two drugs. There’s some evidence this produced systematic differences between the two groups - for example, patients in the control group were 3x more likely to have had diarrhea (this makes sense; diarrhea is a potential ivermectin side effect, so you probably wouldn’t give it to people already struggling with this problem). Also, the control group was twice as likely to be getting corticosteroids, maybe a marker for illness severity.

This might sound concerning, except if you’ve actually read the paper, and have noticed that the authors have provided 33 p-values for baseline characteristics. Scott probably eyeballed it, saw that three of them are below the magic p=0.05 threshold, and made up some stories to go along with his observations.

Notice that Scott doesn’t bother to apply Carlisle’s test, nor does he link to someone else who did. He does not bother to tell us what baseline we should expect in a non-randomized trial and whether 3/33 “statistically significant” characteristics is something we should be concerned about. He also doesn’t seem to notice he’s dealing mostly with dichotomous (not continuous) variables, to which Carlisle’s method doesn’t apply. Remember, this is the exact error that Sheldrick made, but at least Sheldrick showed us his work, so it could be refuted. Scott is content to say there were “systematic differences between the two groups” and leave it at that.

Hint: if you have a biased coin that comes up heads 5% of the time, and you flip it 33 times, you’re 23% likely to get heads at least three times. Is this the rigorous calculation that answers the question of systematic differences? No, and I have enough respect for the complexity of the problem to say this without hesitation. It is, however, more rigorous than whatever Scott used to support his claim in the article.

III. Elalfy et al.

Let’s look at a third case where Scott levies harsh criticism at a paper, focusing on “demographic differences between the groups of the sort which make the study unusable.” In fact, his treatment of this paper is bad enough that we should probably go line-by-line.

Elalfy et al: What even is this? Where am I?

As best I can tell, this is some kind of Egyptian trial. It might or might not be an RCT; it says stuff like “Patients were self-allocated to the treatment groups; the first 3 days of the week for the intervention arm while the other 3 days for symptomatic treatment”. Were they self-allocated in the sense that they got to choose? Doesn’t that mean it’s not random?

Scott starts out confused about whether this trial is an RCT. His confusion is somewhat puzzling, given that the paper says it’s “non-randomized” in several places. In particular:

• …in the abstract

• …in the first line of section 2

• …in the first line of section 3.2

• …at the end of the discussion section. They literally have the following sentence: “Study limitation: the groups were not randomized and the drug combination does not have an established in vitro mechanism of action and remains exploratory.”

How else were the authors supposed to make this clear? Anywho, let’s move on.

Aren’t there seven days in a week? These are among the many questions that Elalfy et al do not answer for us.

The next claim he makes is potentially plausible. Why do the authors divide the week into two sets of three days? I will guess that—since Egypt is a Muslim country—Friday is pretty much off-limits in terms of work, but it would be good to clarify that. Not the sort of thing you throw a trial away for, though.

The control group (which they seem to think can also be called “the white group”) took zinc, paracetamol, and maybe azithromycin. The intervention group took zinc, nitazoxanide, ribavirin, and ivermectin.

Scott makes a special note that they call the control group “the white group.” This is written in one place in the paper as a parenthetical added for context. It’s not like the paper keeps switching terminology, so it feels petty to highlight that as some sort of flaw.

There were very large demographic differences between the groups of the sort which make the study unusable, which they mention and then ignore.

Given that Scott is confused as to whether this paper is an RCT or not, it’s hard to know what he was expecting to see in the demographics. I suspect he sees a number of p-values standing out in the baseline demographics, but doesn’t realize that since the number of patients is small, there are only so many ways the results could be configured, and a string of low or high p-values is not an automatic conclusion that the paper is somehow flawed. Remember: this was exactly Sheldrick’s error with the Marik paper, but here I’m not even sure, because he seems uncertain if he should approach it as a randomized trial or not, which would invert what is expected in the demographics of the patient groups.

In any case, Scott launches his accusation without a formal analysis (once again), so it’s hard to know the supporting argument for his claim.

The researchers do note that there are differences between the groups—as they should—but they did not claim or attempt to randomize. They spell it out: "However, patients on supportive treatment are more likely to be health care workers, unknown exposure, early moderate severity, and have low mean oxygen saturation than the other group." Are any of these factors of the kind that might affect the outcome? Scott doesn’t even get into that, but I don’t quite see how they would, unless we’re worried about biasing the outcome against ivermectin.

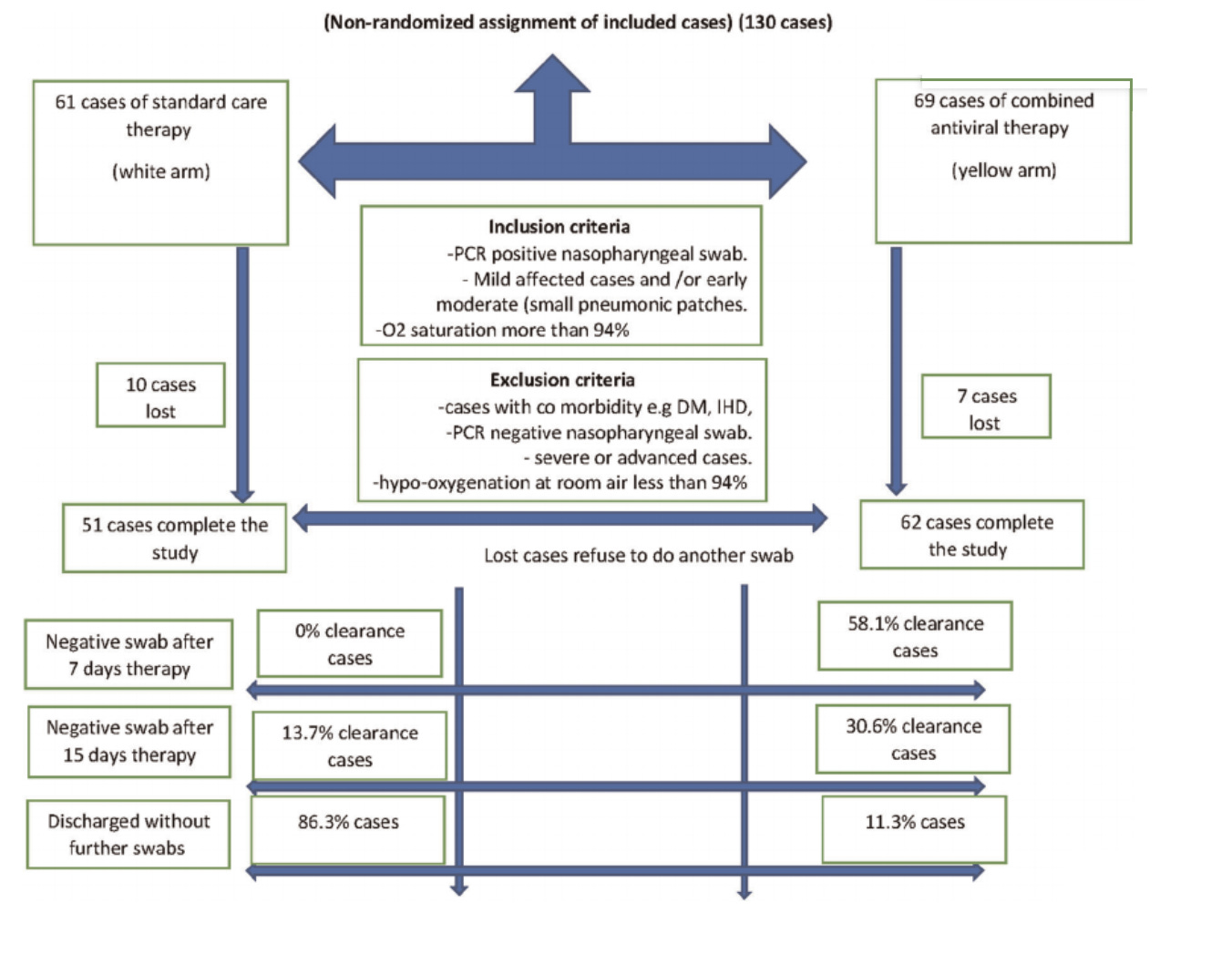
From there, they follow this normal and totally comprehensible flowchart:

I’ll grant that this isn’t a high-quality flowchart, though it is possible to understand what is being described. If we shot scientists for messy diagrams, we wouldn’t have too many left. I will also note that the text at the top of this diagram constitutes the fifth place in the paper where the authors clarify “non-randomized assignment.”

There is no primary outcome assigned, but viral clearance rates on day seven were 58% in the yellow group compared to 0% in the white group, which I guess is a strong positive result.

The registration of the trial on clinicaltrials.gov has a very specific primary outcome assigned, which matches what the paper writes: “Trial results showed that the clearance rates were 0% and 58.1% on the 7th day and 13.7% and 73.1% on the 15th day in the supportive treatment and combined antiviral groups, respectively.” It seems that Scott wants to see the words “primary outcome” somewhere in the paper in order to withhold his criticism, but I’m not aware of any such rule. Where this matters is the registration, and that’s where it’s clearly spelled out.

This table…

…looks very impressive, in terms of the experimental group doing better than the control, except that they don’t specify whether it was before the trial or after it and at least one online commentator thinks it might have been before,

Here we have a case where Scott echoes an accusation he got from “at least one online commentator.” He doesn’t bother to tell us who that is. A search of Twitter returned nothing, so I have no idea who he has in mind here and what exact concern was raised. Admittedly, the paper could more clearly denote this, though the obvious expectation of table 2 in similar publications is that it would be reporting on results after the treatment, not before. Regardless, the paper clearly writes that gastrointestinal upset seems to be the main side-effect of the treatment, which matches the nausea and abdominal pain differences in the treatment group.

in which case it’s only impressive how thoroughly they failed to randomize their groups.

What’s more impressive is that the authors are getting accused of failing to randomize their non-randomized trial.

Overall I don’t feel bad throwing this study out. I hope it one day succeeds in returning to its home planet.

To sum up, we have three cases where Scott’s criticisms of Elalfy have a kernel of truth, though it tends to be weaker than the original claims Scott makes:

• Dividing the week into two sets of three days without clarifying what happens on the 7th is confusing

• Figure 1 could have been designed much more clearly

• Table 2 should have been clearly denoted as relating to post-treatment data

Each of these have obvious default explanations, and perhaps communicating with the authors would actually produce clear answers. However, the far stronger criticisms are either ill-defined or flat-out wrong:

• No primary endpoint defined

• Investigators failed to randomize groups properly

• Large differences in baseline demographics between groups invalidate the study

What’s more, the study is published in a pretty well-established, high-impact journal which Scott does note as a positive for other studies, but it doesn’t seem to warrant a mention here.

Conclusion

John Carlisle built the ballistic missile of academic footguns, one requiring sensitive handling to avoid getting the user into deep trouble. Kyle Sheldrick has been attempting to follow in those footsteps—with the tools of Carlisle and others in hand—deployed with a varying degrees of success. When he faithfully applies the techniques of others, his results tend to be as reliable as the underlying frameworks. When he improvises his own variations of the known methodologies, things go entirely off the rails.

Much like he does with the claims of Gideon Meyerowitz-Katz, Scott does not approach Sheldrick’s work critically, and seems completely oblivious to the statistical critiques of Sheldrick’s work. Not only does he repeat—and even exaggerate—Sheldrick’s claims, he also attempts to emulate him, making claims about the demographic characteristics of various papers, and opining on what they say about the validity of the research.

What started as a moderately useful tool in the hands of an expert has been turned into an all-purpose slime blaster, used to generate costless, unsupported insinuations about the work of scientists from around the world, by applying cookie-cutter heuristics far removed from the original narrow test that Carlisle published.

---

This is a public peer review of Scott Alexander’s essay on ivermectin, of which this is the sixth part. You can find an index containing all the articles in this series here.